Scilab for Uncertainty Quantification

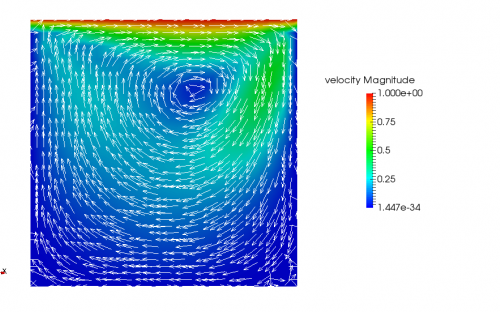
Numerical simulations are the scientific tool used to predict a physical phenomenon without empiric observations. The underlying model is the link between the real environment and the virtual settings, thus its accuracy influences the reliability of the entire simulation. Even if the model can be refined ensuring better results, a certain lack of knowledge could characterize it through uncertainties of the parameters involved. These uncertainties can be due to intrinsic volatility or incomplete knowledge of the quantities considered.

Uncertainty Quantification is a fundamental step towards validation and certification of numerical methods used for critical decisions in presence of uncertainties. Among all stochastic methods, in engineering the non-intrusive ones are more suitable, since it is not possible to modify kernels of well-known and strengthened commercial tools.

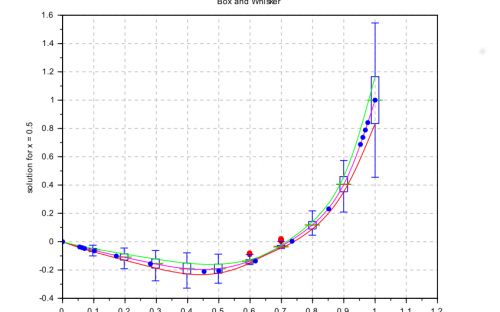
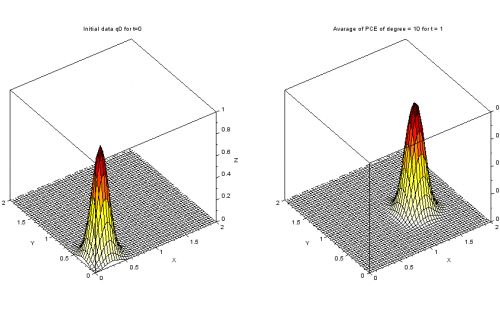
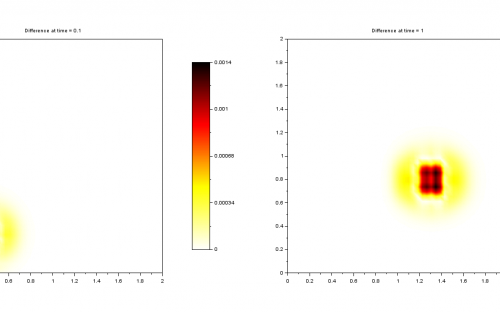
The Polynomial Chaos Expansions (PCE) method is a good mathematical tool to perform this kind of analysis since it allows to drastically reduce the number of simulations and, consequently, the amount of computational time and resources.

Scilab offers a specific toolbox for Non-Intrusive Spectral Projection (NISP), which collects all routines for computing either the univariate or multivariate PCE. Moreover, the user can customize several features of the decomposition and deal with post-processing analysis, such as computations of statistics of the output, samplings and sensitive analysis.

This technique was studied by Gregorio Pellegrini during an internship at Enginsoft S.p.A. This was the starting point for investigating the theoretical properties of PCE and features of NISP approach, which were the core of Gregorio’s thesis Polynomial Chaos Expansion with applications to PDEs for the Master's Degree in Mathematics at University of Verona.