Contribution by Giovanni Conforti - Fellow of the graduate program Berlin Mathematical School
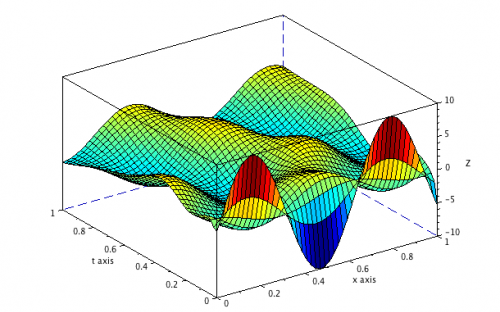
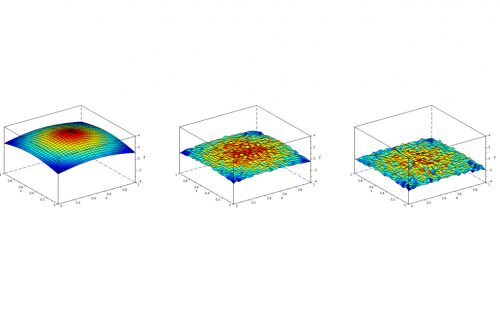
In this work it is described and implemented in Scilab a stochastic numerical algorithm to solve elliptic PDEs with special focus on the heat equation. The algorithm is based on the celebrated Feynman-Kac representation formula. This formula reduces the problem of solving the heat equation to the computation of expected values of functionals of the sample path of the Brownian motion.
Thanks to Monte Carlo methods such expectations can be computed efficiently, thus providing a numerical scheme to solve the PDEs.
The aim of the work is twofolded: beside bringing the attention to such approximation schemes, by discussing both theoretical aspects and simulations in comparison with other PDE solvers, we introduce the main tools that Scilab offers to tackle problems arising from stochastic modeling.
A good property of this method is that it does not suffer of the curse of dimensionality.
A possible application of this technique is to solve pricing problems in financial mathematics (e.g. Black and Scholes PDE).
| Attachment | Size |
|---|---|
 Solving elliptic PDEs in Scilab with the Feynman-Kac formula | 646.68 KB |
