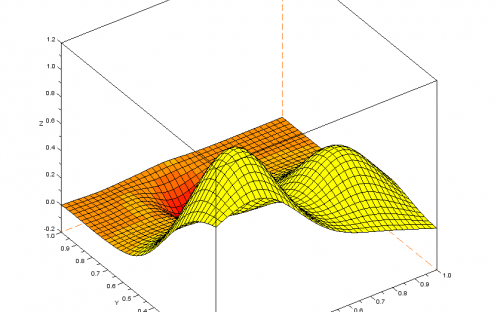
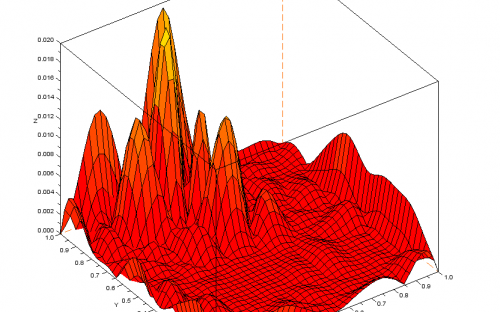
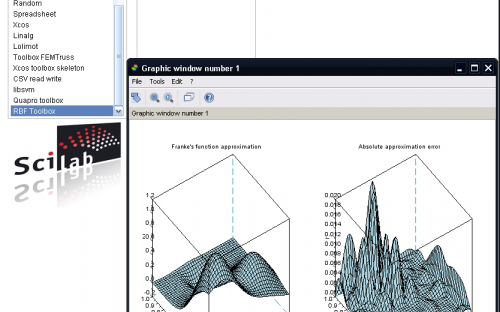
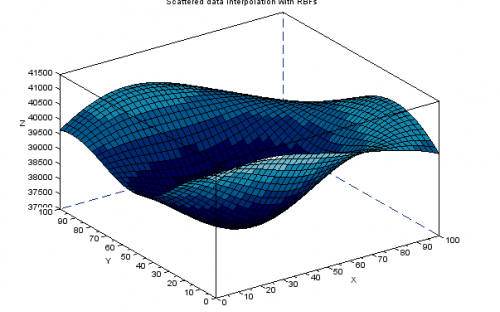
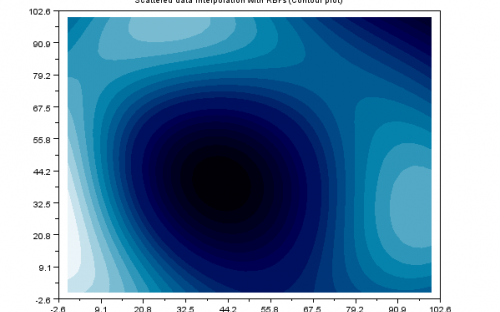
The aim of this work is to develop a Scilab toolbox where Radial Basis Functions are used for scattered data interpolation. We shape our toolbox to be a powerful instrument to analyze data sets coming both from real life applications and industry. The main advantage of using RBFs is that this class is very large, allowing to model various situations.
Nevertheless, there exists a general theory that ensures high tractability of RBFs models and there is empirical evidence that such models give good predictions even with little data. Furthermore the independence of mesh-free discretizations from a mesh permits to eliminate the costs of mesh generation, that is still the most time consuming part of any mesh-based numerical simulation.
This toolbox allows to create an interpolation model based on scattered data from physical or computer experiments. Here, an experiment is a collection of pairs of input and respective evaluation values. The input is likely to be high dimensional, whereas the measurements have to be scalars. Computation with high dimensional data is an important issue in many areas of science and engineering in which many traditional interpolation methods can either not handle such problems or be limited to very regular situations.
We have chosen Scilab with a double motivation. The first one is that it is an advanced and robust language that guarantees robustness and quick prototyping. In addition, it is an open source software, making our work available for free to any member of the community and industrial partners. The toolbox is the final result of a master thesis in Mathematics at Padua University.
The complete Scilab toolbox is available for free but only to registered users. For downloading the toolbox visit: Registered Users Area.
| Attachment | Size |
|---|---|
| 1.04 MB |